| ページ・行 | 誤 | 正 | 備考 | |
| 第13刷でも未修正のもの | ||||
| p.iv | 3.4.2節 | 3.4.2*節 | 20.5.10 読者のご指摘 | |
| p.23,24,25,26,43,53,61, 96,98,99,100,123,147, 148,149,165,166,194, 198,205,222 |
ページ下部のURL | http://www.f.waseda.jp/moriya/books/DM/ | 20.5.10 読者のご指摘 | |
| p.37↓2 | N3 | N | 20.8.27 上村拓也氏のご指摘 | |
| p.37↑6 | ∃z∈R+ | ∃z∈R | 20.8.27 上村拓也氏のご指摘 | |
| p.57↓9 | f(0,n-1) n>0のとき 脚注 |
f(0,n-1)+1 n>0のとき 脚注は削除 |
20.5.30 小柴健史氏のご指摘 | |
| p.70 問3.4 | Dom(A)=Range(A)=A | Dom(R)=Range(R)=A | 20.9.28 上村拓也氏のご指摘 | |
| p.239↓3 | P(空集合)=1-P(Ω)=1 | P(空集合)=1-P(Ω)=0 | 20.8.20 村上慎治氏のご指摘 | |
| p.250↑1 | g-1({0,1,2})={1,2} | g-1({0,1,2})={0,1,2} | 20.6.10 上村拓也氏のご指摘 | |
| p.251↓16 | 1/2+1/(2x)+√(x2+1), 1/2, 1/2+1/(2x)-√(x2+1) | 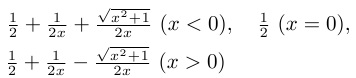 |
20.6.10 大谷直輝氏のご指摘 | |
| p.253 問1.77(5) | B∪(A+{0}A+)* | B∪(A+{0})+A*∪A+ | 20.6.10 上村拓也氏のご指摘 | |
| p.256↑12 | A|V| | 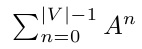 |
20.6.28 小柴健史氏のご指摘 | |
| 第12刷でも未修正のもの | ||||
| p.74↑1,2 | 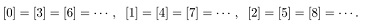 |
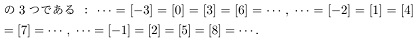 |
18.4.14 | |
| p.75↓1 | 表わす | 表す | 18.4.14 | |
| p.76↓8 | 一般に, | 一般に,mとnが互いに素の場合, | 18.4.14 | |
| p.96↑6 | (2{a,b,c},≦) | (2{a,b,c},⊆) ⊆は $\subseteqq$ | 18.4.30 | |
| p.96↑5 | 直線 | 線分 | 18.4.30 | |
| p.96↑4 | (R,≦)は・・・できない. | (この文は削除する) | 18.4.30 | |
| p.138↓3 | 正則2分木・・・高さは優勝までに・・・ | 2分木・・・高さは(試合数ができるだけ公平の場合)優勝までに・・・ | 2018.5.9 | |
| p.179 定理5.7↑4 | どんな論理式 | 恒真でも恒偽でもないどんな論理式 | 18.2.5 | |
| p.181↑14 | 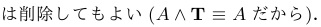 |
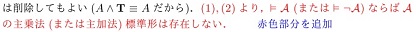 |
18.2.5 | |
| p.211 | 中央の図 | 修正した図 | 18.6.6 | |
| pp.228-229 | nPr (3か所) | n! | 坂間千秋氏のご指摘による 19.4.15 | |
| p.240↑7 | ・・・において,A=・・・ | において,B={HH,HT,TH} とするとき,A=・・・ | 18.5.26 | |
| 第9刷でも未修正のもの | ||||
| p.99↓1 | チャーチ・ロッサー関係 | チャーチ・ロッサー関係(合流性) | 14.5.28(用語補足) | |
| p.99↑12 | チャーチ・ロッサーである | チャーチ・ロッサー関係である(合流性を持つ) | 14.5.28(用語補足) | |
| p.120 ↑9 | ドイツ人 | オーストリア生 | 15.9.1 | |
| p.123 ↑7 | ∪,+,ー,× | ∪,+,× | 15.11.2 | |
| p.127 ↓1 | p≧1 | p≧3 | 15.11.2 | |
| p.127 ↓4 | p = 1, 2 のときは明らか. | 削除 | 15.11.2 | |
| p.141↑2 | できることが知られている | できる(なぜか?) | 14.12.3 | |
| p.142↓3 | 対応している | 対応するように描く | 14.12.3 | |
| p.163, p.164 | procedure Dijkstara と定理4.24 | 訂正 | 15.12.18 | |
| p.171↓1 | 数学的でないことも | 一見数学的でないことも | 15.1.14 | |
| p.172↑0 | 文章を追加 | 定理5.2の証明と同様な考え方で次の定理も証明できる. | 15.1.14 | |
| p.173↓1 | 補題5.3 | 定理5.3 | 15.1.14 | |
| p.175↓3 | 文章を追加 | 問5.9補を見よ. | 15.1.14 | |
| p.177↓17,18 | (5),(6)を1行にする(1行減らすため) | 15.1.14 | ||
| p.177↑0 | 問5.9補 を追加 | 例5.4(4)から分かるように,p.175の双対の定義は曖昧である. 再帰的に曖昧でない定義を与えよ. | 15.1.14 | |
| 以下の誤りは第8刷で修正しました (2013.9) | ||||
| p.52 ↑11 | 0 not⊆ M | 0 not∈ M | 13.4.8 | |
| p.55 | 再帰的定義の説明 | より数学的な説明を補足しました(参考程度) | 13.5.10 | |
| p.69 ↓2 | 任意の自然数 m, n | 任意の自然数 n | 13.5.28 | |
| 以下の誤りは第7刷で修正しました (2013.1) | ||||
| p.124↓2,3 | 1回ずつ通って出発点に戻ってくる | 1回ずつ通る | 12.11.23 | |
| p.125↓1 | q≦2 | q≦3 | 12.11.23 | |
| p.127 脚注↑2 | グラフのこと | 有向グラフのこと | 12.12.7 | |
| 各所 | メンゲル(Menger) | メンガー(Menger) | ネイティブスピーカーに確認 12.8.1 |
|
| p.116↓9 | したがって,互いに接続もしていない | すなわち,B,Cのどの頂点も連結していない | 12.11.10 | |
| p.116↑7〜6 | 最後に,定理の主張をpに関する帰納法で証明する. p=1, q=0 のときは自明グラフで連結である。p≧2のとき, | 最後に,定理の主張を証明する. | 杉本徹氏のご指摘 12.4.14 |
|
| p.116↑1 | r=1 | k=1 | 杉本徹氏のご指摘 12.4.14 |
|
| p.117 問4.22 | (反対は自己補グラフ) | (反例は自明グラフ以外の完全グラフ) | 12.5.5 | |
| p.137↑1 | (内点の数)≦(葉の数-1) | (内点の数)≧(葉の数-1) | 杉本徹氏のご指摘 12.4.14 |
|
| p.256 問4.2(3) | Δ(G_1) = deg(e) | Δ(G_1) = deg(e) = 4 | 杉本徹氏のご指摘 12.4.14 |
|
| p.257 問4.2(7) | G_1 =〜 G_2 [注: =〜 は同型を表す記号(=の上に〜)] |
G_1 - {e} =〜 G_2 | 杉本徹氏のご指摘 12.4.14 |
|
| 以下の誤りは第6刷で修正しました (2011.12) | ||||
| p.6 問1.5 (2) | y<√(1-x)2 または y>-√(1-x)2 | y<√(1-x)2 かつ y>-√(1-x)2 (画像) | 杉本徹氏のご指摘による 11.8.17 |
|
| p.6↑6 | (4) |x|<1/√2 かつ y<1/√2 | (4) |x|<1/√2 かつ |y|<1/√2 | 松田裕貴氏のご指摘による 11.6.6 |
|
| p.10脚注 | Decartes | Descartes | 11.7.18 | |
| p.13↓11 | f(A)を | f(X)を | 杉本徹氏のご指摘による 11.8.17 |
|
| p.15↓13 公式(v) | f-1(f(A))⊆A | f-1(f(A))⊇A (画像) | 杉本徹氏のご指摘による 11.8.17 |
|
| p.21 問1.25 (4) | f-1({3,2,1} | f-1({3,2,1}) | 杉本徹氏のご指摘による 11.8.17 |
|
| p.21 問1.26 (1) | f-1(f(A))⊆A | f-1(f(A))⊇A (画像) | 杉本徹氏のご指摘による 11.8.17 |
|
| p.64 ↓3 例3.1 (4) | X×X | 2X×2X | 杉本徹氏のご指摘による 11.8.17 |
|
| p.109 中央右側の図 | v_i=v_j, v_{i+1}=v_{j+1} | v_i=v_{j+1}, v_{i+1}=v_j | 迎諒氏のご指摘による 11.2.12 |
|
| p.185 | 例5.7図 | 訂正した図 | 11.8.15 | |
| p.224↑15 | 3桁の正整数 | 3桁の正整数(0で始まるものも含む) | 天野一幸氏のご指摘による 11.7.2 |
|
| p.236(5箇所)、p.237(2箇所)、p.239(3箇所) | 根源事象 | 根元事象 | 11.8.28 | |
| p.250 問1.5 (3) | 必要条件でも十分条件でもない | 必要条件 | 杉本徹氏のご指摘による 11.8.17 |
|
| p.250 問1.15 (1) | f(100)=992 | f(100)=1002 | 杉本徹氏のご指摘による 11.8.17 |
|
| p.250 問1.15 (2) | f-1(81)=9, g-1(81)=10, f-1(18)は存在しない |
f-1(81)={9}, g-1(81)={10}, f-1(18)=φ (空集合) (画像) |
杉本徹氏のご指摘による 11.8.17 |
|
| p.251 問1.24 (5)(iv) | 1+1/x+√(1+x2) (x>0), 1/2 (x=0), 1+1/x-√(1+x2) (x<0) | 1/2+1/2x+√(x2+1) (x<0), 1/2 (x=0), 1/2+1/2x-√(x2+1) (x>0) | 11.9.4 | |
| p.256 問3.27 (11) | 推移的× 同値関係× | 推移的○ 同値関係○ | 杉本徹氏のご指摘による 11.8.17 |
|
| p.256 問3.32 (3) | maxA=21, supA=5460 | maxAは存在しない, supA=10920 | 杉本徹氏のご指摘による 11.8.17 |
|
| p.266 問6.47(1) | {赤,青,白,小,中,大} | {(赤,小),(青,中),(白,大)} | 天野一幸氏のご指摘による 11.7.2 |
|
| 以下のものは第5刷で修正しました(2010.12) | ||||
| p.13↑7 | f の値域といい,Range f で | f の値域あるいは像といい,Range f あるいは Im f で | 補足 10.9.22 |
|
| p.31 問1.63(2) | ¬(p∨¬q)⇒¬p | ¬(q∧¬q)⇒¬p | 問題の変更 10.8.7 |
|
| p.51↓1 | 完全帰納法を使って・・・ | いろいろな数学的帰納法を使って・・・ | 誤解のない表現に修正 10.11.26 |
|
| p.51↑12〜13 [基礎] | |x|=0 のとき,・・・でもあるから,λ∈A*B. | x0∈X なる長さ最小の x0 を考えると x0∈B (そうでないとすると x0∈AX より x0=ay なる a∈A, y∈X が存在する.λ not∈A であるから |y|<|x0| であり,|x0| の最小性に反す).B⊆A*B であることより x∈A*B. | 10.5.8 | |
| p.51↑11 | |x|>0 のとき. | |x|>|x0| のとき. | 10.5.8 | |
| p.58↓4 | f(0)=1 | f(0)=0 | 迎諒氏のご指摘による 10.8.7 |
|
| p.69 公式(x) | (R*S*)* ... | (R*◯ S*)* ... | 10.6.11 | |
| p.71↑3 | 与えられたとき | 全射のとき | 10.6.25 | |
| p.139↑15 | Σ内点v(vの子供の数-1) と考える | Σ内点v(vの子供の数) と考える | 09.12.11 | |
| p.196 定理5.7' 主乗法標準形 | Σ | Π | 10.3.3 | |
| p.252 問1.63(2) | ¬(p∨¬q)⇒¬p | ¬(q∧¬q)⇒¬p | 迎諒氏のご指摘によって問題を変更 10.8.7 |
|
| p.253↓11 問1.71(6)解答 | {0,00,000,...} | {λ,0,00,000,...} | 迎諒氏のご指摘による 10.7.27 |
|
| p.256↓6 問3.32(2) | 60∨55=660, 60∧55=5 | 60∨55=660, 60∧55=5, 13∨31=403, 13∧31=1 | 迎諒氏のご指摘により、補足した 10.12.1 | |
| p.257↓8 | (6) 7 | (6) 10 | 中村柚樹氏のご指摘による 10.10.21 |
|
| p.257↓8 | (9) v2 と v5 | (9) v2, v5, v6 | 中村柚樹氏のご指摘による 10.11.19 |
|
| 以下のものは第4刷で修正されました(2009.12) | ||||
| p.12問1.7(4) | 次の但し書きを追加: (ただし、A に関する補集合を考えよ) | 09.2.4 | ||
| p.15公式(v)左式 | f-1(f(A))⊇A | f-1(f(A))⊆A | 09.2.26 | |
| p.21問1.24(2) | R→R | R→R+ | 09.9.3 | |
| p.21問1.26(1) | f-1(f(A))⊇A | f-1(f(A))⊆A | 09.2.26 | |
| p.31問1.63(2) | ¬(p∨¬q)⇒¬p | ¬(q∧¬q)⇒¬p | 09.4.14 | |
| p.97問3.43(2) | n \sqsubseteqq m ⇔(def) n<m かつ・・・
({1,2, ..., 10}, \sqsubseteqq) のハッセ図 |
n \sqsubset m ⇔(def) n<m かつ・・・
({1,2, ..., 10}, \sqsubset*) のハッセ図 (注) 定義の \sqsubseteqq の等号を削除。半順序を、\sqsubseteqq から \sqsubset* へ変更 | 09.6.21 | |
| p.115 ↑5 | したがって,G' が連結・・・ | deg(v)=p-1 なら明らかに G は連結.deg(v)≦p-2 のとき,G' が連結・・・ | 09.10.16 | |
| p.120 定理4.7の証明 | ↓4: G は切断辺を含むので G には・・・ | G は切断辺を含むので $G \cong K_2$ または G には・・・ (さらに、証明に補足説明を加えた) |
09.11.14 | |
| p.125 ↑3 | |E(Qn| = n2n-1 の直後に追加 | ,どの頂点の次数も n | 09.11.22 | |
| p.134 ↓14 | が導かれ, | が導かれ(しかも,まだたどられていない辺が残っているかもしれない), | 09.12.4 | |
| p.172 定理5.1 (2) | A∨B≡B∧A | A∨B≡B∨A | 09.9.3 | |
| p.251問1.61(3) | T | TでもFでもない | 09.5.4 | |
| p.252問1.63(2) | ¬(p∨¬q)⇒¬p | ¬(q∧¬q)⇒¬p | 09.4.14 | |
| 以下のものは第3刷で修正されました(2008.12) | ||||
| p.31問1.64(6) | (p∧¬p)⇒p∨q∨r∧¬s | (p∧¬p)⇒(p∨(q∧¬q)∨¬p) (注: 初学者向けに、⇒の右辺の値が定まるものに変更しました) |
文屋信太郎氏のご指摘による 08.10.10 |
|
| p.35表(xvii) | ∀x[P(x)∨Q(x)] ⇔ ∀x[¬P(x)∧¬Q(x)] | ∀x¬[P(x)∨Q(x)] ⇔ ∀x[¬P(x)∧¬Q(x)] | 読者の方からのご指摘による 08.11.7 | |
| p.82↓4 | (3) 自然数の間の2項関係|を, | (3) 0 以外の自然数の間の2項関係 | を, | 08.6.30 | |
| p.105↓2 | (4,4)グラフ | (5,4)グラフ | 08.9.29 | |
| p.189(VIII) | |= ∃x(A∨B)→∃xA∨∃xB | |= ∃x(A∧B)→∃xA∧∃xB | 08.11.20 | |
| 以下のものは第2刷で修正されました(2007.12) | ||||
| p.6↓7 | 問1.1 (9) ・・・∃y・・・ | 問1.1 (9) ・・・∃y∈N・・・ | 淡誠一郎氏の御指摘による 07.8.30 | |
| p.31↓6 | ∀x∈N∀y∈N∃x∈N[x=y-z] | ∀x∈N∀y∈N∃z∈N[x=y-z] | 淡誠一郎氏の御指摘による 07.8.13 | |
| p.52↓8〜9 | ・・・整列順序の原理という.次の定理は・・・述べている. | ・・・整列順序の原理といい,数学的帰納法と密接な関係がある. | 07.4.16 | |
| p.52↓11〜15 | (帰納法の原理 ⇒ 整列順序の原理) ・・・ | (帰納法の原理 ⇒ 整列順序の原理) F := {m∈N | M⊆N で m∈M なら M は最小元を持つ} と定義すると F=N であることを帰納法で示す.まず,(基礎) 0∈M なら,0 は M の最小元であるから 0∈F.次に,(帰納ステップ) n∈F ⇒ n+1∈F を示す.n+1∈M⊆N なら M が最小元を持つことを示せばよい.0∈M なら 0 が最小元.0 \not∈M なら,n∈M' := {n | n+1∈M} なので M' には最小元 s が存在し,s+1 が M の最小元. | 07.4.16 | |
| p.65↓1〜2 | 有向グラフと呼び,3.4節で詳しく述べる | 3.4節で詳しく述べる「有向グラフ」も参照のこと | 06.7.8 | |
| p.83↓8 | R∩R-1=idA=φ | R∩R-1=R∩idA=φ | 06.7.8 | |
| p.83↑8 | R⊇idA ならば R-1⊇idA であることに注意すると, | 行頭に追加 06.7.8 | ||
| p.83↑5 | idA=φ | R∩idA=φ | 06.7.8 | |
| p.97↑6 | ({0,1, ..., 10}, |) | ({1,2, ..., 10}, |) | 07.7.29 | |
| p.116↓9 | 隣接していない | 隣接していない(したがって、互いに接続もしていない) | 06.10.30 | |
| p.123↑7, 8 | + は結合律を ・・・(中略)・・・ はいずれも可換で結合律 | ∪,+,-,×はいずれも可換で結合律 | 中村真人氏の御指摘による 07.1.27 | |
| p.123↓14 | G10=K1 | G10:=K1 | 06.11.25 | |
| p.123↓15 | 直和は | 直和(や、頂点が明示されていない和)は | 06.11.25 | |
| p.123↓15〜16 | 定義できるものとし,差の定義では G2 を | 定義できるものとする.また,G2 は | 06.11.25 | |
| p.123↓17 | 除去したグラフ G1-v, G1-e は | 加除したグラフ G1±v, G1±e は | 06.11.25 | |
| 4.3.1項ウェブ版 | 上記p.123の訂正に準じる修正 07.1.27 | |||
| p.141 系4.18 | Gが平面的グラフ | Gが平面グラフ | 06.12.1 | |
| p.143↓3 | ,u, v が隣接点でなく,かつ | 「2辺 uw, wv があり」の直後に挿入 06.11.25 | ||
| p.229↓8〜10 | 26!/(13! 13!), 13個の→, 13個の↑ | 16!/(8! 8!), 8個の→, 8個の↑ | 淡誠一郎氏の御指摘による 07.8.21 | |
| p.234↑7,↑5 | 13×13 ・・・ 13個の飛車 ・・・ 攻撃しあわない | 9×9 ・・・ 9個の飛車 ・・・ 互いに進路を妨げない | 淡誠一郎氏の御指摘による 07.8.21 | |
| p.265↑14 | 13! | 9! | 淡誠一郎氏の御指摘による 07.8.21 | |
| p.265↑13 | (2n-1)(2n-2)(2n-5)・・・3・1 | (2n-1)(2n-3)(2n-5)・・・3・1 | 淡誠一郎氏の御指摘による 07.8.21 | |
| p.265↑10 | 2×52C2 | 2×50C2 | 淡誠一郎氏の御指摘による 07.8.21 | |